|
|
之前我在系列第1篇文章深度学习的可解释性 XAI-1-Introduction中提到了,对于模型输出Y= Model ( x_{test} ; θ ) = Model ( x_{test} ; θ(X_{train}) ) ,我们可以讲往3个方向上解释:
- 对测试数据 x_{test},解释模型依据哪些特征产生Y。
- 对训练数据集 X_{train},解释 额外使用某个训练数据 x_{train}^i 去训练模型,对测试数据x_{test}的输出Y的影响。
- 对模型参数 \theta ,解释具体某个模型结构学到了哪些”概念“。
本文先对第1个方向展开,讲讲主流的基于梯度的方法(第3部分)、CAM(和GradCAM)相关的方法(第4部分)、和基于扰动的方法(Perturbation based method)(第5部分)。这些方法都能追溯到一个哲学思想 -- 通过回答一个反事实问题,来提供解释(第2部分)。
1. 测试数据的特征的定义
我们想要解释输入的测试数据的各个特征,对于输出的影响。那么我们首先就要定义什么是“特征”。
(1)对于视觉模型,输入是图片,所以其特征可以是 像素 / patch / superpixel / instance mask
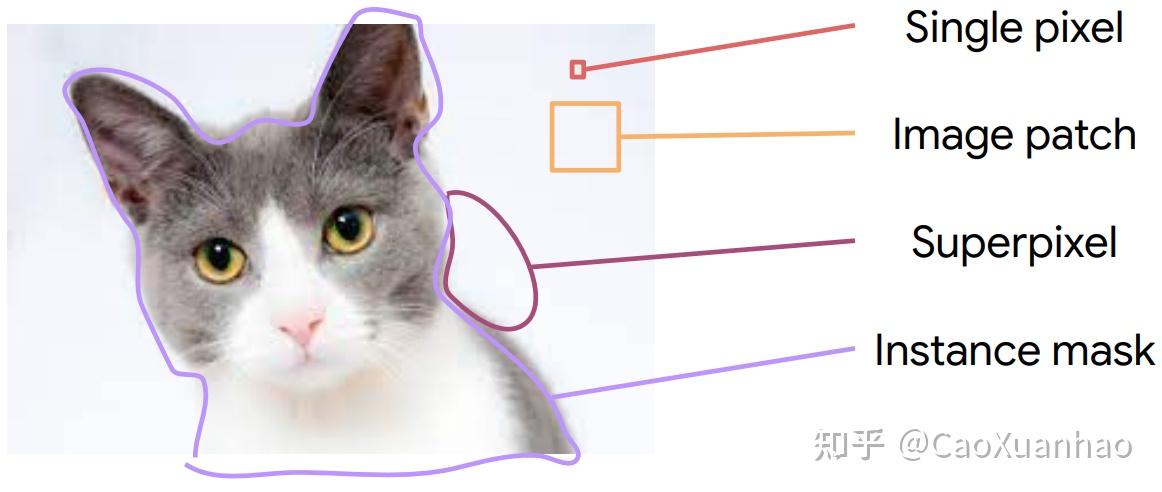
其中patch就是Vision Transformer中的输入patch。instanece mask是实例分割中的一个完整实例。Superpixel是一组像素,但有着相似的颜色或者边缘特征;它比像素的粒度要大,但比物体的粒度要小。
(2)对于语言模型,token/词 就是特征

知道了什么是特征之后,就可以来研究模型根据哪些特征来做分类。主流的方法有很多,但大部分都基于一个思想(或者可以用这个思想去理解) -- 反事实解释。
2. 对特征的反事实解释(Counterfactual reasoning over features)
在XAI中,想要解释一个神经网络的行为,可以回答由反事实思想提出的2个问题:(1)如果输入x的特征被改变了,输出y会怎么变?

如果输入猫猫图中的耳朵特征消失了,输出分类标签y会怎么变?
如果成功地回答了这个问题,那么我们就得到了“如果输入x的特征被改变了,输出y的变化程度”,进而可以用这个“变化程度”作为该输入特征的重要性,这就是我们期望的“解释”。
回答这个反事实问题,催生出了基于梯度的和基于特征图的可解释性算法(文章第3、4部分)。
(2)如果输出y变了,是输入x中的哪个特征导致的这种变化?

如果输出分类标签y变成了“狗”,那么是哪些输入特征变化,导致了这个输出的变化?
回答这个反事实问题,催生出了基于扰动的可解释性算法(文章第6部分)。
按照这个思想,我们先来考虑通过回答第1个反事实问题来做解释--“如果输入x的特征被改变了,输出y会怎么变?”。首先我们考虑把像素(pixel)作为特征来解答这个问题,然后在第4部分再进一步考虑用superpixel作为特征。
3. 基于梯度的方法
3.1 Gradient as explanation
我们可以对每个像素分别做些小扰动(small pixel perturbation),如果输出变化大的话,就说明这个像素很重要。那么要如何计算这个变化呢?
最简单的方法是计算扰动后的输出 f(x+h) 和扰动前的输出 f(x) 的差值 f(x+h)-f(x) ,如果这个差值大,则说明这个像素重要。这需要计算2次前向传播。
但有个更聪明的方法:我们可以用梯度来近似这种差值: f'(x)=\lim_{h \rightarrow 0}{\frac{f(x+h)-f(x)}{h}} !

对每个像素都做上面那种计算,就可以得到我们想要的解释了:
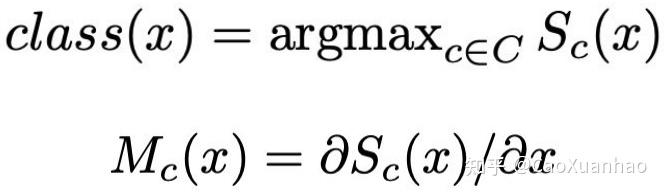
它与输入图片的尺度一样,所以可视化之后,长这样:

右边是input gradient的结果
结果比较noisy。那有没有可以让它更平滑的方法呢? \rightarrow Smoothgrad
3.2 Smoothgrad: Smoother gradients
它的计算方法很简单,就是
给输入图片加随机噪音: x+\varepsilon ,这样做很多次之后取平均就行:

但SmoothGrad的结果还是不Smooth,有没有更进一步的方法呢?
3.3 积分梯度(Integrated Gradients,IG)
回忆一下,之前提到的Gradient方法的本质是近似 局部的小扰动
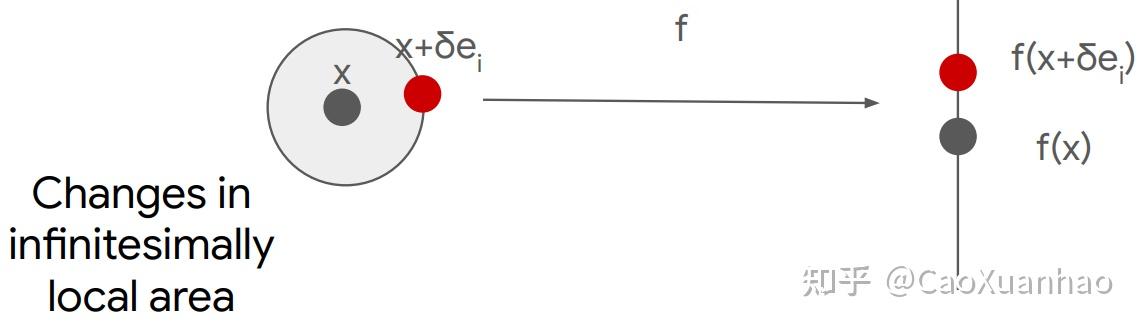
而SmoothGrad也是近似 局部的小扰动,只不过扰动次数更多一些:
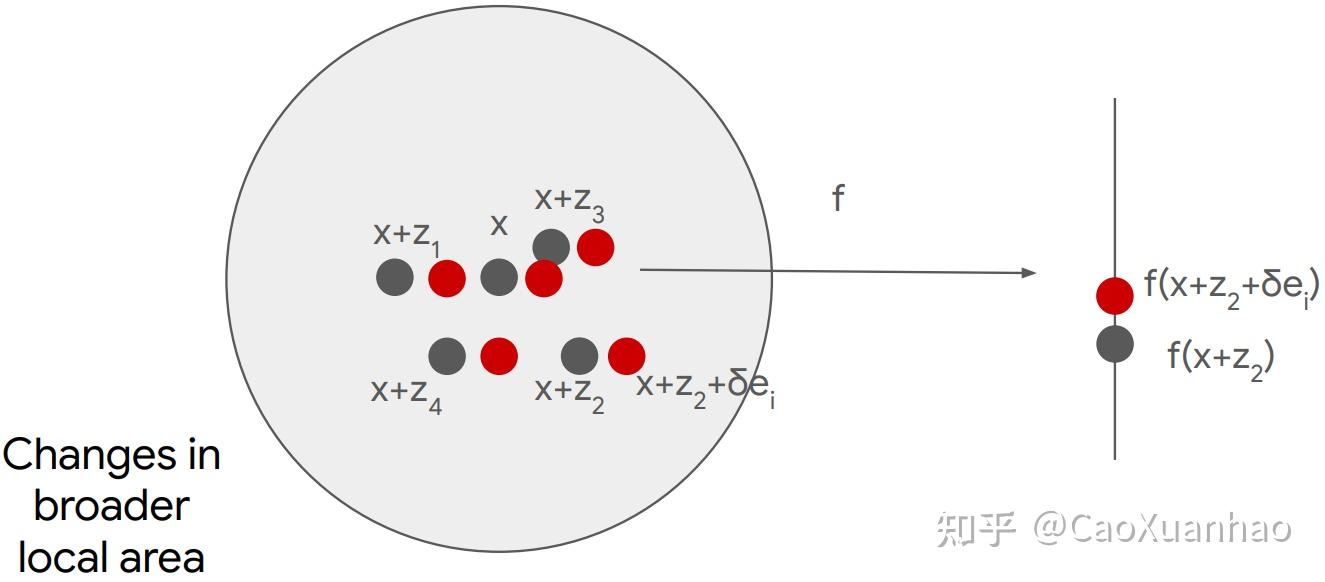
可以发现,它们都是用“局部扰动(local perturbation)”这一种扰动方法,来回答反事实问题。扰动之后,得到的新输入 x+\delta 是在原输入 x 的局部小邻域内,比如加了点小噪音。再把所有扰动后得到的x+\delta求梯度做平均。

那么,我们能不能不只局限在“局部扰动”这一种扰动方法,用其它的扰动方法呢。这就是Integrated Gradients使用的扰动方法 --“全局扰动(global perturbation)”。
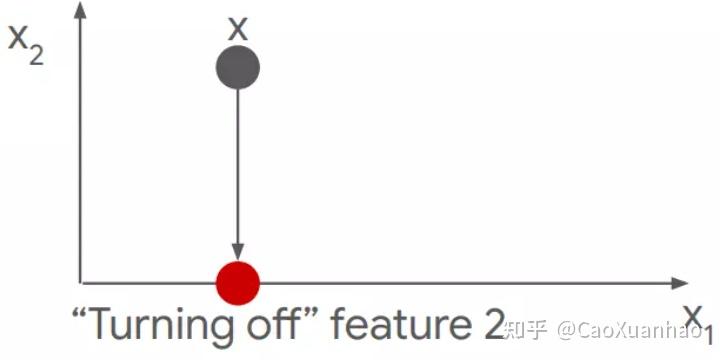
“全局扰动”的特殊之处在于,扰动之后,得到的新输入 x' (baseline image)中的某个feature的信息被完全抹除了,比如图片中整个物体都被抹除,换成黑色的像素。
与Smoothgrad类似,Integrated Gradients也是把所有扰动后得到的可能的 \tilde{x} 求梯度做平均,只不过这些\tilde{x}是原输入 x ,新输入 x',以及它们俩中间插值得到的\tilde{x}=x+\alpha(x'-x), \alpha \in [0,1]。(当 \alpha=0 时, \tilde{x}=x ;当 \alpha=1 时, \tilde{x}=x' )
写成数学公式,就是:
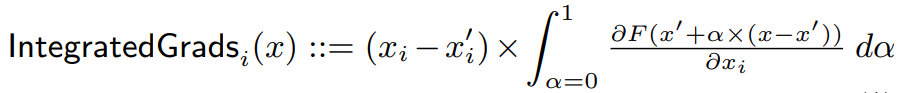
下标i指的是第i个像素。对所有的像素都计算即可得到整个图片的。
一般用采样(sampling)来近似这个积分:

注意我们这里在前面加上了一个(x-x')项,这是为了让它满足"Completeness Axiom" -- 所有像素的IG值加起来等于输出的变化:
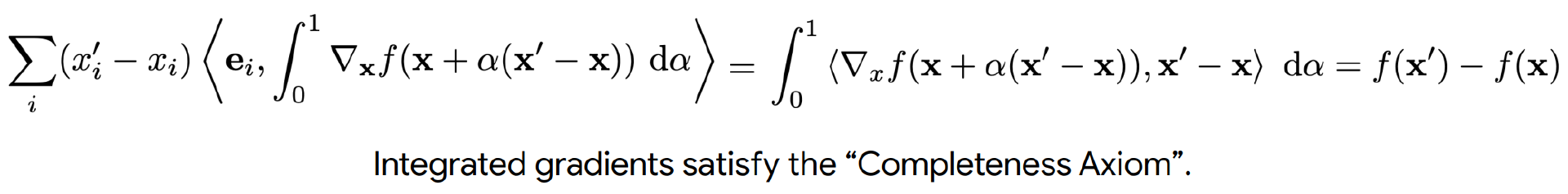
Pixel-wise contributions for x must sum up to the difference between the current model output f(x) and some baseline output f(x') 最终效果比普通的Gradient好,更平滑,但仍旧非常noisy:

这类方法的好处是每个像素都有一个值,来表示这个像素对输出y的贡献程度,但坏处就是结果非常noisy。这是所有基于梯度的方法的最大缺陷,很难解决,而且成因仍旧是个谜。
而绕开这种缺点的方法是基于特征图(feature map)的方法 -- CAM based method。
4. 缘起特征图(feature map)
在语义分割(Sementic Segmentation)的开山之作中[1],作者们发现在训练完一个CNN分类模型之后,它的特征图(feature map)可视化之后能定位物体的重要性,所以可以拿来做语义分割/物体检测/可解释性。这个发现奠定了可解释性领域与语义分割、物体检测领域各种错综复杂的关系。

图:对于一个CNN分类模型(上图),不看它的FC部分,只看CNN部分(下图),那么最后几层得到的特征图可视化之后(右下角的那个 heatmap )就是能捕捉物体显著部分的 saliency map。这个 saliency map 即可以用于可解释性,也能用于 Semantic segmentation 和 Object detection,区别在于对图像的粒度
但问题是,这个特征图太粗了,是superpixel级别的,而语义分割要的像素级别的结果。那怎么办呢?
作者们和后来的学者给出的办法就是,直接在特征图(feature map)之后再接一个CNN,输入特征图,输出细粒度(pixel level)的语义分割结果。于是就有了经典的U-Net:
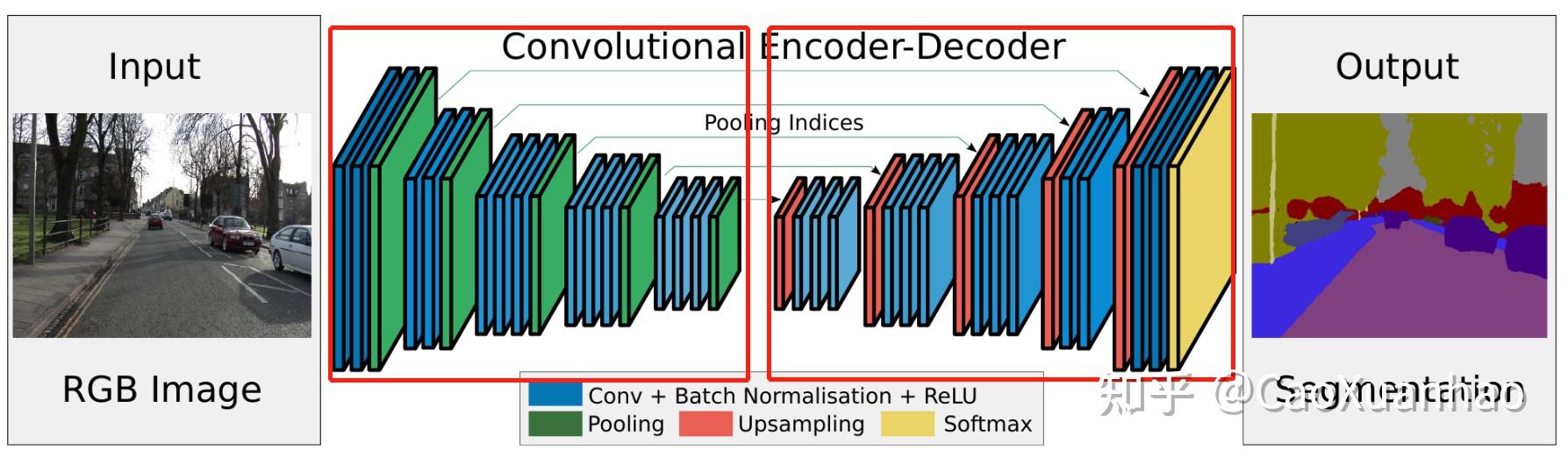
但这样改动了原来的CNN。而在可解释性领域,我们对粗细粒度不是很在意;而且也不想对CNN进行改动,而是试图让它保持不变,只用特征图 去做解释。那么问题就简化很多了,就不用在后面接一个CNN Decoder了,直接可视化原始的特征图就行:用binear interpolation上采样到原始输入图像大小,再可视化。于是就有了CAM系列的方法(CAM based method)。
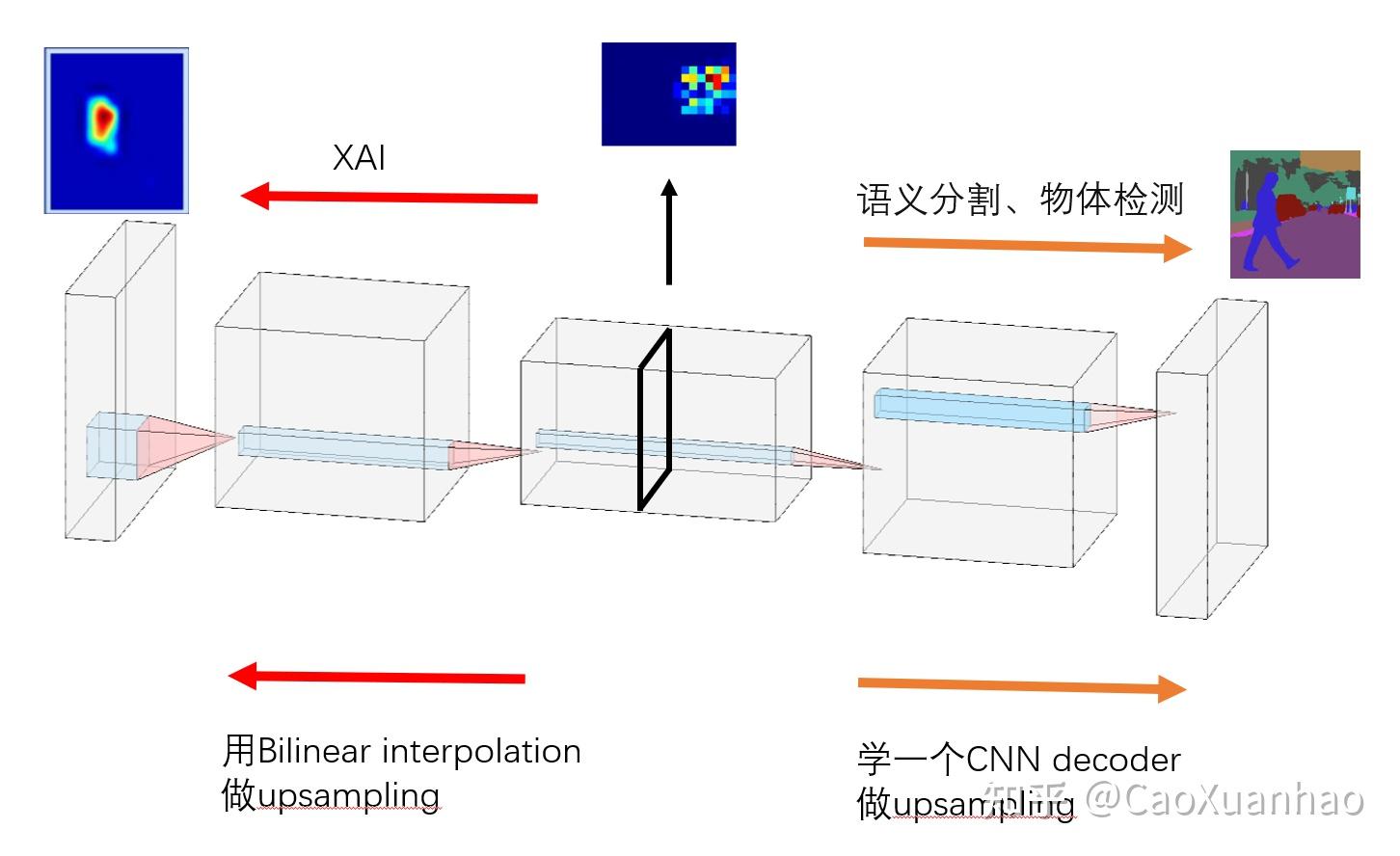
特征图是个好东西,很多任务都能用到它
4.2 CAM与Grad-CAM
CAM系列的方法的核心思想很简单,就是对所有通道(Channel)的特征图 加权求和!
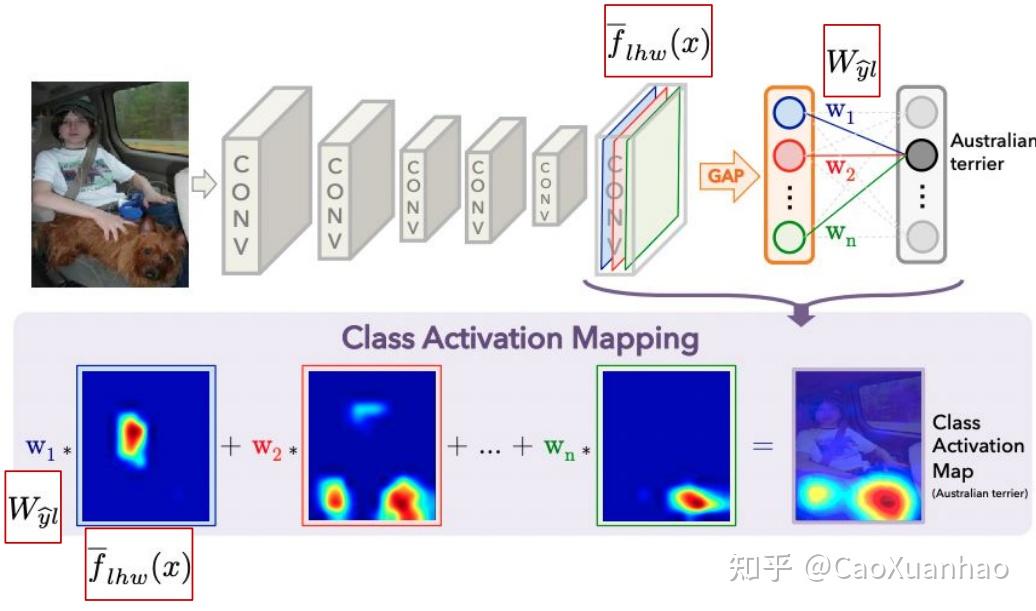
每个特征图可视化之后都可以作为可解释性,但可能突出了物体的不同部分;而CAM将其加权求和,结果更好更稳健。
一般取神经网络最后一层的特征图(feature map),以输出y到这些特征图(feature map)的梯度的平均值作为权重,加权求和。这时候CAM的数学公式为:
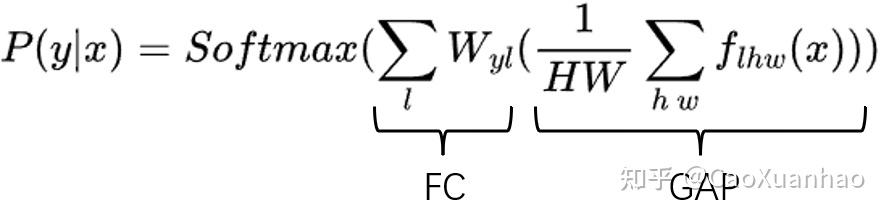
其中 P(y|x)是给定输入 x ,输出类别是 y 的概率;f_{lhw}是特征图,有 l 个通道,空间尺寸是 h\times w 。原始的CAM论文针对的CNN是对特征图使用GAP(global average pooling)后,再加一层全连接层FC。这时 W_{yl} 指的是FC中第 l 个通道到第 y 个输出的权重。调整累加的次序后得到:

但不是所有的CNN最后都会接一层GAP,往往是非线性的(比如多层FC),所以Grad-CAM对此做了改进,把W_{yl}用梯度取代:
W_{yl} = \frac{1}{HW}\sum_{h w}^{}\frac{\partial y}{\partial f_{lhw}}
也就是用输出 y 到第 l 个通道的特征图 f_{lhw} 的梯度来代替该通道的重要性,作为权重。
最终的结果长这样:

这类方法的好处是能够不noisy,能够突出物体整体。但坏处是我们只能得到superpixel(特征图中的元素是superpixel级别的)层面的解释,需要用线性插值(bilinear interpolation)来求出最终的结果。
同时这种superpixel层面的解释意味着,对每个superpixel,我们有一个数值来衡量其重要性,也就意味着我们在superpixel层面来回答那个反事实问题,去做解释了。
5. 缺点
现在所有的可解释性方法都有一个更本质的缺点,就是它们或多或少,都只考虑了线性化之后的简化的模型。
(1)基于梯度的可解释性方法把整个模型 f 全部线性化来解释
本来深度学习模型 f是非线性的,但基于梯度的可解释性方法只考虑了f的一阶泰勒展开作近似: \begin{align} f(x) &= f(x_0)+(x-x_0)\frac{\partial f}{\partial x} + O((x-x_0)^2) \\ &\approx f(x_0)+(x-x_0)\frac{\partial f}{\partial x} \\ & = x\frac{\partial f}{\partial x}+(f(x_0)-x_0\frac{\partial f}{\partial x}) \end{align}
这样输入 x 对输出 f(x) 的影响就完全可以用梯度 \frac{\partial f}{\partial x} 来解释了。
(2)基于特征图的可解释性方法(CAM based method)把整个模型 f 部分线性化来解释
比如在GradCAM中,我们用梯度W_{yl} = \frac{1}{HW}\sum_{h w}^{}\frac{\partial y}{\partial f_{lhw}} 作为通道的权重。但实际上因为特征 f_{lhw} 到输出 y 是非线性的,其影响力也是非线性的,但这部分我们也用一阶泰勒展开作近似,所以其影响力才是梯度W_{yl} = \frac{1}{HW}\sum_{h w}^{}\frac{\partial y}{\partial f_{lhw}} 。
不难发现,越接近线性的模型,可解释性越好,但效果就越差。越复杂的模型,效果越好,但可解释性越差,以至于我们不得不将其简化(线性化)来解释。但这种线性化,解释的是简化后的模型,而不是原模型,使得解释的真实性受到了质疑。
那么有没有不用简化(线性化)模型的可解释性方法呢?那我们可以考虑回答第2个反事实问题--“如果输出y变了,是输入x中的哪个特征导致的这种变化?”,这种思路引出了基于扰动的可解释性算法。
6.基于扰动的方法
(1)这类方法先假设输出变化,比如最小化类别c的输出概率 min_m \ f_c(\Phi(x,m)) ,或者输出类别发生变化(class c的概率小于class d的概率) f_c(\Phi(x,m)) < f_d(\Phi(x,m)) ;
(2)然后探究是哪些输入特征发生了变化(比如给输入 x 乘以一个binary mask m ,来盖住一部分信息 \Phi(x,m)=x\odot m ),导致的这种变化。如果输出变化大,则说明输入 x 中被扰动的部分用来做决策的可能性越大。而这部分特征,就是我们寻找的,可以解释模型行为的特征。
这类算法有很多变体,不过它们的思路都是类似的,都是上面那2步,只是第1部分的目标函数和第2部分擦除信息的函数 \Phi(x,m) 不同而已。我就先介绍其中一个最具代表性的方法--Meaningful perturbations:
Meaningful perturbations (MP)
MP算法考虑解下面一个优化问题,通过优化寻找mask m ,使得输入 x_0 被这个mask处理过后(得到 \Phi(x_0,m) ),模型输出中类别c的概率最小:
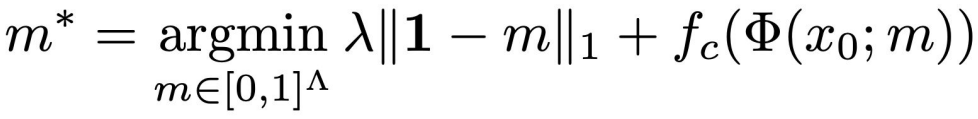
其中m是binary mask,用来擦除输入 x_0 中的特征信息。 f_c 是模型输出类别 c 的概率。第1项 ||1-m||_1 是正则化项,因为我们想要这个mask擦除的面积越小越好(只擦除特征信息,不难把整张图都盖住了);而且也不能是对抗性攻击(adversial attack)中的那种杂乱无章的mask。这里 Φ(x_0 ; m) 可以用很多种方法,而论文中用的是Blurring of image x_0 according to the mask m:
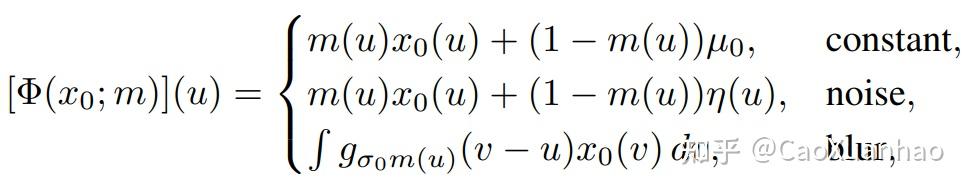
最后的结果长这样:

但这类方法因为要去&#34;找&#34; 导致输出y变化的 输入x变化的部分(即去找哪些mask可以擦除信息,哪个mask盖住的部分就是有效特征),所以一般要求解个优化问题,所以速度会比较慢。而且因为这个搜索空间比较大,往往需要做些近似。还有这些mask往往不像上面那个图那样,一般会有很多噪音(类似adversial attack那样的)。
7. 小结
- 对测试数据的可解释性方法,都试图通过回答2个反事实问题之一来解释 --
- (1)如果输入特征变化了,输出会怎么变?
- (2)如果输出变了,是输入中的哪个特征导致的这种变化?
- 在像素层面上回答问题(1),我们就有了基于梯度的可解释性方法。
- 在superpixel层面上回答问题(1),我们就有了基于特征图(CAM based method)的可解释性方法。
- 但这2类方法都有本质的缺陷,就是或多或少都把原模型线性化来解释。
- 为了避开这个缺陷,我们可以回答问题(2),于是就有了基于扰动的可解释性方法。
Reference
参考
- ^Jonathan Long, Evan Shelhamer, Trevor Darrell. 2015. Fully Convolutional Networks for Semantic Segmentation. In CVPR.
|
|