|
|
复数基本运算
#include <complex>
#include<iostream>
using namespace std;
int main() {
complex<float> a(1, -1); //复数的定义
float a_real = a.real(); //复数取实部
float a_imag = a.imag(); //复数取虚部
std::cout << &#34;复数a:&#34;<< a << std::endl;
std::cout << &#34;复数a的实部:&#34; << a_real << std::endl;
std::cout << &#34;复数a的虚部:&#34; << a_imag << std::endl;
complex<float> b(2, -2);
std::cout << &#34;复数b:&#34; << b << std::endl;
complex<float> c = a + b; //复数加法
std::cout << &#34;c=a+b:&#34; << c << std::endl;
complex<float> d = a*b; //复数乘法
std::cout << &#34;c=a*b:&#34; << d << std::endl;
complex<float> a_conj(a.real(),-a.imag()); //复数共轭
std::cout << &#34;复数a的共轭:&#34; << a_conj << std::endl;
complex<float> f1(0,2);
complex<float> f2 = exp(f1);//用于表达欧拉公式
std::cout << &#34;exp(2i):&#34; << f2 << std::endl;
return 0;
}
复数矩阵求逆
参考:C++实现复数矩阵求逆 matlab inv
matlab2c使用c++实现matlab函数开发配置全解_腾讯数据架构师的博客-CSDN博客_arma-matlab2cpp
#include <iostream>
#include <complex>
using namespace std;
// 矩阵加法 a+b,其中a、b均为n*m型矩阵
double** Add(double** a, double** b, int n, int m) {
double** res = new double* [n];
for (int i = 0; i < n; i++) res = new double[m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
res[j] = a[j] + b[j];
}
}
return res;
}
// 矩阵乘法,a*b,a为n*m型矩阵,b为m*o型矩阵
double** Mul(double** a, double** b, int n, int m, int o) {
double** res = new double* [n];
double temp = 0.0;
for (int i = 0; i < n; i++) res = new double[o];
for (int i = 0; i < n; i++) {
for (int j = 0; j < o; j++) {
temp = 0.0;
for (int k = 0; k < m; k++) {
temp += a[k] * b[k][j];
}
res[j] = temp;
}
}
return res;
}
void swap(double* a, double* b); //声明子程序
// 实数矩阵求逆,返回a的逆,其中a为num型方阵
double** inv(double** a, int num)
{
int* is, * js, i, j, k;
int n = num;
double temp, fmax;
double** tp = new double* [num];
for (int i = 0; i < num; i++) tp = new double[num];
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
tp[j] = a[j];
}
}
is = new int[n];
js = new int[n];
for (k = 0; k < n; k++)
{
fmax = 0.0;
for (i = k; i < n; i++) {
for (j = k; j < n; j++)
{
temp = fabs(tp[j]);//找最大值
if (temp > fmax)
{
fmax = temp;
is[k] = i; js[k] = j;
}
}
}
if ((fmax + 1.0) == 1.0)
{
delete[] is;
delete[] js;
return NULL;
}
if ((i = is[k]) != k)
for (j = 0; j < n; j++)
swap(&tp[k][j], &tp[j]);//交换指针
if ((j = js[k]) != k)
for (i = 0; i < n; i++)
swap(&tp[k], &tp[j]); //交换指针
tp[k][k] = 1.0 / tp[k][k];
for (j = 0; j < n; j++)
if (j != k)
tp[k][j] *= tp[k][k];
for (i = 0; i < n; i++)
if (i != k)
for (j = 0; j < n; j++)
if (j != k)
tp[j] = tp[j] - tp[k] * tp[k][j];
for (i = 0; i < n; i++)
if (i != k)
tp[k] *= -tp[k][k];
}
for (k = n - 1; k >= 0; k--)
{
if ((j = js[k]) != k)
for (i = 0; i < n; i++)
swap(&tp[j], &tp[k]);
if ((i = is[k]) != k)
for (j = 0; j < n; j++)
swap(&tp[j], &tp[j][k]);
}
delete[] is;
delete[] js;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
}
}
return tp;
}
void swap(double* a, double* b)
{
double c;
c = *a;
*a = *b;
*b = c;
}
complex<double>** GetMatrixInverse(complex<double>** src, int n) {
double** A = new double* [n];
double** B = new double* [n];
for (int i = 0; i < n; i++) {
A = new double[n];
B = new double[n];
for (int j = 0; j < n; j++) {
A[j] = src[j].real();
B[j] = src[j].imag();
}
}
double** A1 = inv(A, n);
double** A1B = Mul(A1, B, n, n, n);
double** BA1B = Mul(B, A1B, n, n, n);
double** AjBA1B = Add(A, BA1B, n, n);
double** AjBA1B_1 = inv(AjBA1B, n);
double** A1B_AjBA1B_1 = Mul(A1B, AjBA1B_1, n, n, n);
complex<double>** res = new complex<double> * [n];
for (int i = 0; i < n; i++) {
res = new complex<double>[n];
for (int j = 0; j < n; j++) {
res[j].real(AjBA1B_1[j]);
res[j].imag(-1.0 * A1B_AjBA1B_1[j]);
}
}
return res;
}
int main() {
complex<double>** temp = new complex<double> * [3];
for (int i = 0; i < 3; i++) {
temp = new complex<double>[3];
}
complex<double> t1(1, 0);
temp[0][0] = t1;
temp[2][1] = t1;
temp[2][2] = t1;
complex<double> t2(1, 1);
temp[0][2] = t2;
temp[1][1] = t2;
complex<double> t3(0, 1);
temp[1][0] = t3;
complex<double> t4(2, -1);
temp[0][1] = t4;
complex<double> t5(1, 2);
temp[1][2] = t5;
complex<double> t6(-1, 1);
temp[2][0] = t6;
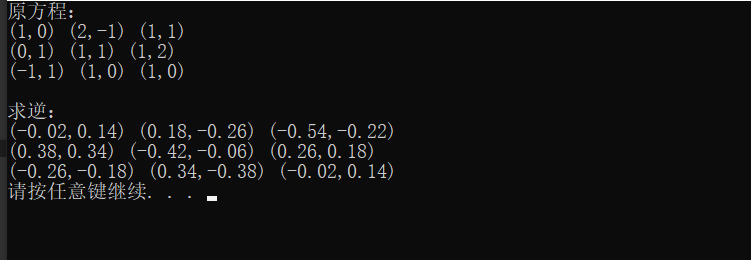
cout << &#34;原方程:&#34; << endl;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << temp[j]<<&#34; &#34;;
}
cout << endl;
}
cout << endl <<&#34;求逆:&#34;<<endl;
complex<double>** res = GetMatrixInverse(temp, 3);
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << res[j] << &#34; &#34;;
}
cout << endl;
}
system(&#34;pause&#34;);
return 0;
}
 |
|